一种回溯的解数独算法
数独是一种逻辑性的数字填充游戏,玩家须以数字填进每一格,而每行、每列和每个宫(即3x3的大格)有齐1至9所有数字。游戏设计者会提供一部分的数字,使谜题只有一个答案。
算法步骤
- 1、扫描整个9x9宫格,根据已有的数字找出每一个空格能够填充的所有数字,若出现某一个空格没有能够填充的数字,则进行回溯。
- 2、选择拥有最少能够填充数字的空格,从能够填充的数字中选取一个数填入该空格,将填入的空格位置和剩余的能够填充的数字压入历史堆栈
- 3、重复1直至所有空格均被填充,则完成
回溯操作
- 1、从历史堆栈弹出一个元素,若堆栈为空,则该数独无解。
- 2、若弹出的元素的剩余可填充数字个数为0,则将该元素所纪录的空格从宫格中删除,重复1,否则,从剩余的可填充数字中选取一个重新填入该空格。
代码实现
class Sudoku(object):
"""
Sudoku solver
"""
def __init__(self, matrix):
self.matrix = matrix
self.history_stack = []
def _push_history(self, pos, val_list):
self.history_stack.append([pos] + val_list)
def _pop_history(self):
if len(self.history_stack) > 0:
if len(self.history_stack[-1]) > 1:
self._set_pos(self.history_stack[-1][0],
self.history_stack[-1].pop())
else:
tem = self.history_stack.pop()
self._set_pos(tem[0], 0)
self._pop_history()
else:
raise Exception("out of history_stack")
def _set_pos(self, pos, val):
self.matrix[pos // 9][pos % 9] = val
def _get_pos(self, pos):
return self.matrix[pos // 9][pos % 9]
def _get_available(self, pos):
ret = [1, 2, 3, 4, 5, 6, 7, 8, 9]
s_x = (pos // 9) * 9
for i in range(s_x, s_x+9):
if i == pos:
continue
val = self._get_pos(i)
if val != 0 and val in ret:
ret.remove(val)
s_y = pos % 9
for i in range(s_y, 81, 9):
if i == pos:
continue
val = self._get_pos(i)
if val != 0 and val in ret:
ret.remove(val)
box_y = pos // 27
box_x = (pos % 9) // 3
box_start = 27 * box_y + 3 * box_x
for i in range(box_start, box_start+21, 9):
for j in range(i, i+3):
if j == pos:
continue
val = self._get_pos(j)
if val != 0 and val in ret:
ret.remove(val)
return ret
def _pos_to_xy(self, pos):
return pos // 9, pos % 9
def _find_enter(self):
enter = -1
available_list = []
for i in range(81):
val = self._get_pos(i)
if val != 0:
continue
tem_list = self._get_available(i)
if len(tem_list) == 0:
raise Exception("matrix error trace back")
if enter == -1 or len(tem_list) < len(available_list):
enter = i
available_list = tem_list
return enter, available_list
def display(self):
for line in self.matrix:
print(line)
def solver(self):
while 1:
try:
enter, available_list = self._find_enter()
except Exception:
self._pop_history()
continue
if enter == -1:
return self.matrix
self._set_pos(enter, available_list.pop())
self._push_history(enter, available_list)
测试
测试我用了所谓的芬兰数学家因卡拉花费3个月设计出了世界上迄今难度最大的九宫格游戏
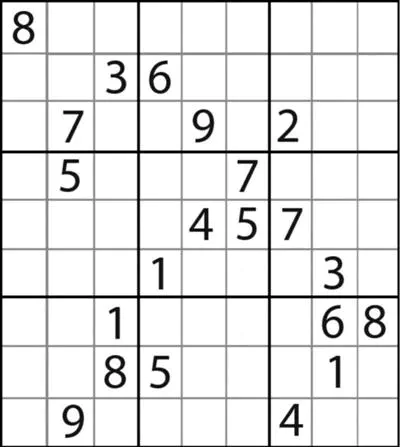
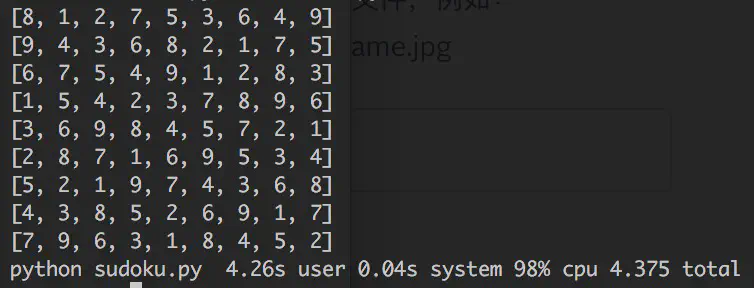
实际用时四秒左右,应该很有很大的优化空间